推荐阅读:凸优化常见技巧 做题笔记-KingPowers 以及文中的推荐文章。
我们要解决的问题一般都是类似于区间分拆问题,其 2D-1D 递推式一般都类似:
f k , i = opt { f k − 1 , j + w ( j + 1 , i ) } f_{k,i}=\operatorname{opt}\{f_{k-1,j}+w(j+1,i)\}
f k , i = o p t { f k − 1 , j + w ( j + 1 , i ) }
其中 w ( i , j ) w(i,j) w ( i , j ) g ( k ) : = f ( n , k ) g(k):=f(n,k) g ( k ) : = f ( n , k ) g ( k ) g(k) g ( k )
proof. \text{proof.} proof.
尝试证明 g ( k − 1 ) + g ( k + 1 ) ≥ 2 g ( k ) g(k-1)+g(k+1)\geq 2g(k) g ( k − 1 ) + g ( k + 1 ) ≥ 2 g ( k ) k − 1 k-1 k − 1 [ a 1 , d 1 ] , … , [ a k − 1 , d k − 1 ] [a_1,d_1],\dots,[a_{k-1},d_{k-1}] [ a 1 , d 1 ] , … , [ a k − 1 , d k − 1 ] k + 1 k+1 k + 1 [ b 1 , c 1 ] , … , [ b k + 1 , c k + 1 ] [b_1,c_1],\dots,[b_{k+1},c_{k+1}] [ b 1 , c 1 ] , … , [ b k + 1 , c k + 1 ] k k k j j j c j + 1 ≤ d j c_{j+1}\leq d_j c j + 1 ≤ d j d k − 1 = n d_{k-1}=n d k − 1 = n a j < b j + 1 ≤ c j + 1 ≤ d j a_j<b_{j+1}\leq c_{j+1}\leq d_j a j < b j + 1 ≤ c j + 1 ≤ d j j j j
[ a 1 , d 1 ] , … , [ a j − 1 , d j − 1 ] , [ a j , c j + 1 ] , [ b j + 2 , c j + 2 ] , … , [ b k + 1 , c k + 1 ] ⟺ [ b 1 , c 1 ] , … , [ b j + 1 , d j ] , [ a j + 1 , d j + 1 ] , … , [ a k − 1 , d k − 1 ] [a_1,d_1],\dots, [a_{j-1},d_{j-1}],[a_j,c_{j+1}],[b_{j+2},c_{j+2}],\dots,[b_{k+1},c_{k+1}]
\iff [b_1,c_1],\dots ,[b_{j+1},d_j],[a_{j+1},d_{j+1}],\dots,[a_{k-1},d_{k-1}]
[ a 1 , d 1 ] , … , [ a j − 1 , d j − 1 ] , [ a j , c j + 1 ] , [ b j + 2 , c j + 2 ] , … , [ b k + 1 , c k + 1 ] ⟺ [ b 1 , c 1 ] , … , [ b j + 1 , d j ] , [ a j + 1 , d j + 1 ] , … , [ a k − 1 , d k − 1 ]
于是 2 g ( k ) 2g(k) 2 g ( k ) 2 g ( k ) ≤ g ( k − 1 ) + g ( k + 1 ) 2g(k)\leq g(k-1)+g(k+1) 2 g ( k ) ≤ g ( k − 1 ) + g ( k + 1 )
Q.E.D. \text{Q.E.D.} Q.E.D.
以上文字是我之前在 cnblogs 上写的,自以为掌握了一个数学模型能够不用脑子利用 wqs 二分切题的方法,可这样的数学模型真的足够普适吗?显然不!也许王钦石在发明这个方法的时候确实是从 dp 问题中归纳出来的数学模型,但经过后人的推广之后,wqs 二分的应用范围已经不仅仅局限于 dp。更普适的模型如下:
对于定义在自然数域上、值域为正整数的凸包 f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x ) f ( 0 ) f(0) f ( 0 ) δ f ( x ) \delta f(x) δ f ( x ) k k k f ( x ) − x k f(x)-xk f ( x ) − x k − k -k − k f ′ ( 0 ) f'(0) f ′ ( 0 )
那我之前写的真的就一无是处吗?显然不!把那一大段贴上是因为这个二级结论非常常用,能方便我们做题。
[国家集训队] Tree I
给定一个无向带权连通图,每条边是黑色或白色,求一棵最小权的恰有 k k k ∣ V ∣ ≤ 5 × 1 0 4 , ∣ E ∣ ≤ 1 0 5 |V|\leq 5\times 10^4,|E|\leq 10^5 ∣ V ∣ ≤ 5 × 1 0 4 , ∣ E ∣ ≤ 1 0 5
设 f ( x ) f(x) f ( x ) x x x f ( x ) f(x) f ( x ) p p p p p p
Luogu P4983 忘情
算得上板子中的板子了,直接搬运我之前写的。
设 f i f_i f i i i i i i i s i = ∑ j = 1 i a i s_i=\sum_{j=1}^ia_i s i = ∑ j = 1 i a i
f i = min j = 1 i − 1 { f j + ( s i − s j ) 2 + c } = min { f j + s i 2 − 2 s i s j + s j 2 + c } = min { − 2 s j × s i + s j 2 + f j } + s i 2 + c f_{i}=\min_{j=1}^{i-1}\{f_j+(s_i-s_{j})^2+c\}
\\ = \min\{f_{j}+s_i^2-2s_is_j+s_j^2+c\}
\\ = \min\{-2s_j\times s_i +s_j^2+f_j\}+s_i^2+c
f i = j = 1 min i − 1 { f j + ( s i − s j ) 2 + c } = min { f j + s i 2 − 2 s i s j + s j 2 + c } = min { − 2 s j × s i + s j 2 + f j } + s i 2 + c
如果对于某个 c c c m m m c k ck c k c c c c c c m m m c = x c=x c = x m m m c = x + 1 c=x+1 c = x + 1 m m m c = x + 1 c=x+1 c = x + 1 k k k ( x + 1 ) m (x+1)m ( x + 1 ) m O ( n log C ) O(n\log C) O ( n log C )
Luogu P5633 最小度限制生成树
给你一个有 n n n m m m s s s k k k 1 ≤ s ≤ n ≤ 5 × 1 0 4 1\leq s\leq n \leq 5\times 10^4 1 ≤ s ≤ n ≤ 5 × 1 0 4 1 ≤ m ≤ 5 × 1 0 5 1\leq m \leq 5\times 10^5 1 ≤ m ≤ 5 × 1 0 5 1 ≤ k ≤ 100 1\leq k \le 100 1 ≤ k ≤ 1 0 0 0 ≤ w ≤ 3 × 1 0 4 0\leq w\leq 3\times 10^4 0 ≤ w ≤ 3 × 1 0 4
设 f ( x ) f(x) f ( x ) s s s x x x f ( x ) f(x) f ( x )
proof. \text{proof.} proof.
显然对 ∣ T ∣ = 1 , 2 |T|=1,2 ∣ T ∣ = 1 , 2
假设对于 ∣ T ∣ ≤ n |T|\leq n ∣ T ∣ ≤ n ∣ T ∣ = n |T|=n ∣ T ∣ = n e e e e e e T 1 , T 2 T_1,T_2 T 1 , T 2 f T ( k ) = min ( f T 1 ( k 1 ) + f T 2 ( k 2 ) ) f_T(k)=\min(f_{T_1}(k_1)+f_{T_2}(k_2)) f T ( k ) = min ( f T 1 ( k 1 ) + f T 2 ( k 2 ) ) ( min , + ) (\min,+) ( min , + ) T T T □ \square □
于是二分斜率,给 s s s m i d mid m i d
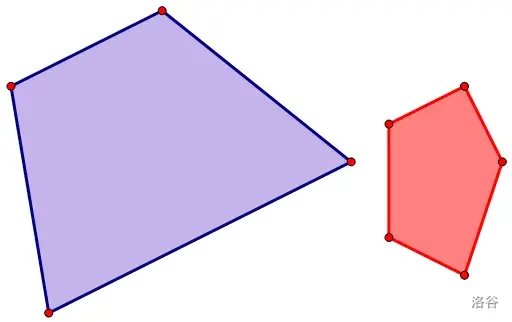
定义是对于两个点集 A , B A,B A , B C = { a + b ∣ a ∈ A , b ∈ B } C=\{a+b|a\in A, b\in B\} C = { a + b ∣ a ∈ A , b ∈ B }
这对于普通的点集来说并没有什么值得研究的,但是对于两个凸包来说就有的搞头了。盗一下经典图。
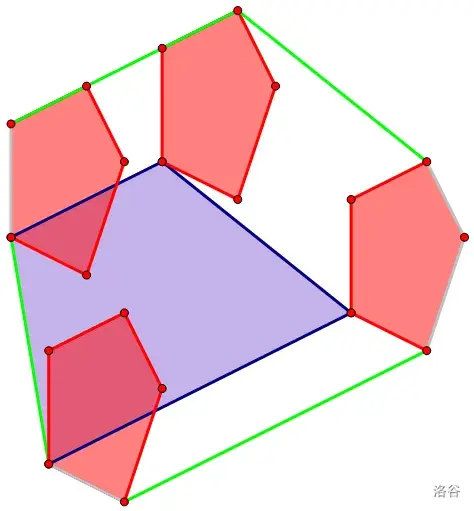
对上面两个凸包做 Minkowski 和,得到新的点集:
发现把边看成向量的话新凸包的边就是把原来两个凸包的边按照斜率排序之后顺次拼接形成的。这非常有用,假设有 f , g f,g f , g O ( ∣ f ∣ + ∣ g ∣ ) O(|f|+|g|) O ( ∣ f ∣ + ∣ g ∣ ) f , g f,g f , g ( min , + ) (\min,+) ( min , + ) h k = min j + k ( f j + g k ) h_{k}=\min_{j+k}(f_j+g_k) h k = min j + k ( f j + g k ) f , g f,g f , g h h h f , g f,g f , g x x x ( min , + ) (\min,+) ( min , + ) ( max , + ) (\max,+) ( max , + )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 inline vector<int > merge (vector<int > a, vector<int > b) int > c;pb (a[0 ] + b[0 ]);int l = 1 , r = 1 ;while (l < a.size () && r < a.size ())if (a[l] - a[l - 1 ] < b[r] - b[r - 1 ]) c.pb (a[l] - a[l - 1 ]), ++l;else c.pb (b[r] - b[r - 1 ]), ++r;while (l < a.size ()) c.pb (a[l] - a[l - 1 ]), ++l;while (r < b.size ()) c.pb (b[r] - b[r - 1 ]), ++r;fo (i, 0 , c.size () - 1 ) c[i] += c[i - 1 ];return c;
2020 ICPC Shenyang R L.Forged in the Barrens
给定数列 { a n } \{a_n\} { a n } k k k k ∈ [ 1 … n ] ∩ Z k\in [1\dots n]\cap \mathbb{Z} k ∈ [ 1 … n ] ∩ Z n ≤ 1 0 5 , a i ≤ 1 0 9 n\leq 10^5,a_i\leq 10^9 n ≤ 1 0 5 , a i ≤ 1 0 9
套路化的设 f i , j f_{i,j} f i , j i i i j j j O ( n 3 ) O(n^3) O ( n 3 ) f i , j , 0 / 1 / 2 f_{i,j,0/1/2} f i , j , 0 / 1 / 2 i i i j j j O ( 1 ) O(1) O ( 1 ) O ( n 2 ) O(n^2) O ( n 2 ) f n f_n f n k k k
然后有一个技巧就是把序列上的 dp 当做区间 dp 去做,设 f l , r , 0 / 1 / 2 , 0 / 1 / 2 , k f_{l,r,0/1/2,0/1/2,k} f l , r , 0 / 1 / 2 , 0 / 1 / 2 , k [ l … r ] [l\dots r] [ l … r ] k k k m i d mid m i d
f l , r , o l , o r , k = max { max ( f l , m i d , o l , o r , k , f m i d + 1 , r , o l , o r , k ) max x + y = k ( f l , m i d , o l , 1 , x + f m i d + 1 , r , 1 , o r , x ) max x + y = k − 1 ( f l , m i d , o l , 0 , x + f m i d + 1 , r , 2 , y ) max x + y = k − 1 ( f l , m i d , o l , 2 , x + f m i d + 1 , r , 0 , y ) f_{l,r,ol,or,k}=\max\begin{cases}
\max(f_{l,mid,ol,or,k},f_{mid+1,r,ol,or,k}) \\
\max\limits_{x+y=k}(f_{l,mid,ol,1,x}+f_{mid+1,r,1,or,x})\\
\max\limits_{x+y=k-1}(f_{l,mid,ol,0,x}+f_{mid+1,r,2,y})\\
\max\limits_{x+y=k-1}(f_{l,mid,ol,2,x}+f_{mid+1,r,0,y})
\end{cases}
f l , r , o l , o r , k = max ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ max ( f l , m i d , o l , o r , k , f m i d + 1 , r , o l , o r , k ) x + y = k max ( f l , m i d , o l , 1 , x + f m i d + 1 , r , 1 , o r , x ) x + y = k − 1 max ( f l , m i d , o l , 0 , x + f m i d + 1 , r , 2 , y ) x + y = k − 1 max ( f l , m i d , o l , 2 , x + f m i d + 1 , r , 0 , y )
m i d mid m i d O ( n log n ) O(n\log n) O ( n log n )
2022 ICPC Nanjing R H.Factories Once More
n n n k k k 1 ≤ k ≤ n ≤ 2 × 1 0 5 1\leq k\leq n\leq 2\times 10^5 1 ≤ k ≤ n ≤ 2 × 1 0 5 [ 1 , 1 0 9 ] [1,10^9] [ 1 , 1 0 9 ]
暴力树背包是设 f u , i f_{u,i} f u , i u u u i i i f u , x = max i + j = x { f u , i + f v , j + w ( u , v ) ⋅ j ⋅ ( k − j ) } f_{u,x}=\max_{i+j=x}\{f_{u,i}+f_{v,j}+w(u,v)\cdot j\cdot (k-j)\} f u , x = max i + j = x { f u , i + f v , j + w ( u , v ) ⋅ j ⋅ ( k − j ) } j ( k − j ) j(k-j) j ( k − j ) ( max , + ) (\max,+) ( max , + ) + w ( u , v ) j ( k − j ) +w(u,v)j(k-j) + w ( u , v ) j ( k − j ) w ( k − 2 j + 1 ) w(k-2j+1) w ( k − 2 j + 1 ) f u , 0 = 0 f_{u,0}=0 f u , 0 = 0 O ( n log 2 n ) O(n\log^2n) O ( n log 2 n )
什么是 slope trick?如图:
用于优化呈分段一次函数状的 dp,当然也要求是凸的,也就是说 g ( x ) = Δ f ( x ) g(x)=\Delta f(x) g ( x ) = Δ f ( x ) g ( x ) g(x) g ( x ) k k k k k k
dp 的设计并非该算法的重点(虽然对于题目至关重要),而凸性证明在闵和的基础上已经有了充足的技术支撑,因此学 slope trick 重点是把转移对差分数组的影响想明白。
CF713C Sonya and Problem Without a Legend 加两个 0
给定 { a n } \{a_n\} { a n } n ≤ 3 × 1 0 5 , 1 ≤ a i ≤ 1 0 9 n\leq 3\times 10^5,1\leq a_i\leq 10^9 n ≤ 3 × 1 0 5 , 1 ≤ a i ≤ 1 0 9
a i ← a i − i a_i\leftarrow a_i-i a i ← a i − i d p i , j dp_{i,j} d p i , j a i ← j a_i\leftarrow j a i ← j d p i , j = min k = 1 j { d p i − 1 , k } + ∣ a i − j ∣ dp_{i,j}=\min_{k=1}^j \{dp_{i-1,k}\} + |a_i-j| d p i , j = min k = 1 j { d p i − 1 , k } + ∣ a i − j ∣ O ( n 2 ) O(n^2) O ( n 2 ) f i ( x ) = d p i , x f_{i}(x)=dp_{i,x} f i ( x ) = d p i , x f ( x ) f(x) f ( x ) ∣ a i − x ∣ |a_i-x| ∣ a i − x ∣ ∣ a i − x ∣ |a_i-x| ∣ a i − x ∣ p p p a i ≥ p a_i\geq p a i ≥ p a i a_i a i a i a_i a i
CF372C Watching Fireworks is Fun 加七个 0
n n n m m m a i a_i a i t i t_i t i x x x b i − ∣ a i − x ∣ b_i-|a_i-x| b i − ∣ a i − x ∣ d d d n ≤ 1 0 9 , m ≤ 2 × 1 0 5 , a i , b i , t i ≤ 1 0 9 n\leq 10^9,m\leq 2\times 10^5,a_i,b_i,t_i\leq 10^9 n ≤ 1 0 9 , m ≤ 2 × 1 0 5 , a i , b i , t i ≤ 1 0 9 t i t_i t i
相当于 ∑ ∣ a i − x ∣ \sum |a_i-x| ∑ ∣ a i − x ∣ d p i , x dp_{i,x} d p i , x i i i x x x d p i , x = ∣ a i − x ∣ + min x − d Δ t ≤ y ≤ x + d Δ t d p i − 1 , y dp_{i,x}=|a_i-x|+\min_{x-d\Delta t\leq y\leq x+d\Delta t}dp_{i-1,y} d p i , x = ∣ a i − x ∣ + min x − d Δ t ≤ y ≤ x + d Δ t d p i − 1 , y f i ( x ) = d p i , x f_i(x)=dp_{i,x} f i ( x ) = d p i , x f ( x ) f(x) f ( x ) min x − d Δ t ≤ y ≤ x + d Δ t d p i − 1 , y \min_{x-d\Delta t\leq y\leq x+d\Delta t}dp_{i-1,y} min x − d Δ t ≤ y ≤ x + d Δ t d p i − 1 , y d d d d d d + ∣ a i − x ∣ +|a_i-x| + ∣ a i − x ∣ [ l , r ] [l,r] [ l , r ] a i ∈ [ l , r ] a_i\in [l,r] a i ∈ [ l , r ] a i a_i a i a i < l a_i<l a i < l a i a_i a i a i > r a_i>r a i > r
[OOI 2025] The arithmetic exercise
给定 { a n } \{a_n\} { a n } m m m x 1 , x 2 , … , x m x_1,x_2,\dots,x_m x 1 , x 2 , … , x m 1 ≤ i ≤ m 1\leq i\leq m 1 ≤ i ≤ m j i j_i j i a j i ← x − a j i a_{j_i}\leftarrow x-a_{j_i} a j i ← x − a j i ∑ a i \sum a_i ∑ a i n , m ≤ 300000 , − 1 0 9 ≤ x i ≤ 1 0 9 n,m\leq 300000,-10^9\leq x_i\leq 10^9 n , m ≤ 3 0 0 0 0 0 , − 1 0 9 ≤ x i ≤ 1 0 9
正着做会导致前面定了符号的 x i x_i x i { k n } \{k_n\} { k n } ∀ i ∈ [ 1 , n ] , 0 ≤ ∑ j = 1 i k i ≤ n \forall i\in [1,n],0\leq\sum_{j=1}^ik_i\leq n ∀ i ∈ [ 1 , n ] , 0 ≤ ∑ j = 1 i k i ≤ n f i , j f_{i,j} f i , j x i x_i x i k i k_i k i j j j d p i , j = max { d p i − 1 , j − 1 + x i , d p i − 1 , j + 1 − x i } dp_{i,j}=\max\{dp_{i-1,j-1}+x_i,dp_{i-1,j+1}-x_i\} d p i , j = max { d p i − 1 , j − 1 + x i , d p i − 1 , j + 1 − x i } j j j d p i , j dp_{i,j} d p i , j − x i , x i {-x_i,x_i} − x i , x i ( max , + ) (\max,+) ( max , + ) − x i -x_i − x i x i x_i x i f i ( j ) = d p i , j f_i(j)=dp_{i,j} f i ( j ) = d p i , j f 0 f_0 f 0 i − 1 → i i-1\rightarrow i i − 1 → i f i − 1 f_{i-1} f i − 1 f i f_i f i i − 1 → i i-1\rightarrow i i − 1 → i ∑ x i \sum x_i ∑ x i f i − 1 f_{i-1} f i − 1 d p i , j = max { d p i , j , d p i − 1 , j − 2 + 2 x i } dp_{i,j}=\max\{dp_{i,j},dp_{i-1,j-2}+2x_i\} d p i , j = max { d p i , j , d p i − 1 , j − 2 + 2 x i } d p i , j dp_{i,j} d p i , j i , j i,j i , j j − 2 → j j-2\rightarrow j j − 2 → j j − 1 → j j-1\rightarrow j j − 1 → j