写写博客,记记术语,方便以后看题解/hanx。
串串感觉和数据结构、DP 都有藕断丝连的关系,但如果把这些知识点分到其他板块里面就让被硬塞进这些字符串知识点的板块过于割裂,所以干脆单拎出来。
说明:本篇中字符串下标从 0 开始。
给一个串,如何求所有的回文半径?
维护覆盖了当前点的右端点最右的回文串,找到当前点关于这个回文串的中心的对称点,直接把它的在这个串内的信息拿到右端点上,剩下的暴力扩展就行了。因为暴力扩展的时候右端点只增不减,所以时间复杂度为 Θ ( n ) \Theta(n) Θ ( n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 #include <cstring> #include <iostream> using namespace std;const int N = 1.1e7 + 10 ;inline bool chk (char c) return c >= 'a' && c <= 'z' ; }int n, f[N];char s[N], c;int main () 0 ] = '~' ;while (chk (c = getchar ())) s[++n] = '|' , s[++n] = c;'|' ;for (int i = 1 , maxr = 0 , mid = 0 ; i <= n; i++)if (i < maxr) f[i] = min (f[2 * mid - i], maxr - i);for (int j = i + f[i] + 1 ; j <= n; j++)if (s[j] == s[2 * i - j]) ++f[i];else break ;if (i + f[i] > maxr) maxr = i + f[i], mid = i;int ans = 0 ;for (int i = 1 ; i <= n; i++)if (f[i] > ans) ans = f[i];return 0 ;
这里主要放一些 01-trie 常见的 trick,并写一写可持久化 01-trie。OI-Wiki 写的太烂了,主要参考了这一篇 。
从高位到低位存储,直接往 01-Trie 里面加数,然后能往另一边走就往另一边走。例题
考虑对答案有贡献当且仅当 1 的个数为奇数,于是从低位到高位存储。
问题来了,如果还让求最大异或该咋办?
答:开两颗呗,卡卡常不就行了?
对于每一位记:
c[i]:当前节点到他爸爸这条边被经过的总次数
w[i]:当前节点为根的子树内所有边权的异或和
然后就自然地有代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void maintain (int u) 0 ;if (ch[u][0 ])0 ]]; 0 ]] << 1 ); if (ch[u][1 ])1 ]];1 ]] << 1 ) | (c[ch[u][1 ]] & 1 ));
然后插入和删除的时候修改当前节点的 w 就行了。代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 void ins (int &u, int x, int dep) if (!u) u = newnode ();if (dep > MAXH) return w[u]++, void ();ins (ch[u][x & 1 ], x >> 1 , dep + 1 );maintain (u);void del (int u, int x, int dep) if (dep > MAXH) return w[u]--, void ();del (ch[u][x & 1 ], x >> 1 , dep + 1 );maintain (u);
考虑加一的操作等价于把从后往前第一个 0 变成一,然后后面的全部异或,这在 01-trie 上就是从低位到高位维护,不断交换左右儿子,直到找到 0。代码:
1 2 3 4 5 6 void add (int u) swap (ch[u][0 ], ch[u][1 ]);if (ch[u][0 ]) add (ch[u][1 ]);maintain (u);
代码中判断 ch[u][0] 是因为你已经交换过一遍左右儿子了。
区间加一就做一遍可持久化就行了。
例题:Luogu P4735 最大异或和
设 s i = ⨂ j = 1 i a i s_i=\bigotimes\limits_{j=1}^i a_i s i = j = 1 ⨂ i a i s n ⊗ s p − 1 ⊗ x s_n\otimes s_{p-1}\otimes x s n ⊗ s p − 1 ⊗ x [ l − 1 , r − 1 ] [l-1,r-1] [ l − 1 , r − 1 ] s p ⊗ ( s n ⊗ x ) s_p \otimes (s_n\otimes x) s p ⊗ ( s n ⊗ x )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <bits/stdc++.h> using namespace std;const int N = 6e5 + 5 , H = 28 ;int n, m, a[N], s[N], rt[N], ch[N * 33 ][2 ], cnt[N * 33 ], tot;void Insert (int u, int pre, int x) for (int i = H; i >= 0 ; i--)1 ;int c = ((x & (1 << i)) ? 1 : 0 );if (!ch[u][c]) ch[u][c] = ++tot;1 ] = ch[pre][c ^ 1 ];1 ;int query (int u, int v, int x) int res = 0 ;for (int i = H; i >= 0 ; i--)int c = ((x & (1 << i)) ? 1 : 0 );if (cnt[ch[u][!c]] - cnt[ch[v][!c]]) u = ch[u][!c], v = ch[v][!c], res += (1 << i);else u = ch[u][c], v = ch[v][c];return res;int main () tie (nullptr )->sync_with_stdio (false );tie (nullptr );for (int i = 1 , x; i <= n; i++) cin >> a[i], s[i] = s[i - 1 ] ^ a[i];for (int i = 1 ; i <= n; i++) rt[i] = ++tot, Insert (rt[i], rt[i - 1 ], s[i]);char op;for (int l, r, val; m; m--)if (op == 'A' )1 ] ^ a[n], rt[n] = ++tot;Insert (rt[n], rt[n - 1 ], s[n]);if (op == 'Q' )if (!l) cout << max (s[n] ^ val, query (rt[r], rt[0 ], s[n] ^ val)) << '\n' ;else cout << query (rt[r], rt[l - 1 ], s[n] ^ val) << '\n' ;return 0 ;
这一块 OI-Wiki 讲得还可以,扳回一城。
定义一个长度为 n n n s s s π [ i ] \pi[i] π [ i ] s [ 1 … i ] s[1\dots i] s [ 1 … i ] π [ 0 ] = 0 \pi[0]=0 π [ 0 ] = 0
π \pi π 暴力时间复杂度是 O ( n 3 ) O(n^3) O ( n 3 )
怎么优化?
随几个串串,把 π \pi π π \pi π i i i π [ i − 1 ] + 1 \pi[i-1]+1 π [ i − 1 ] + 1 n − 1 n-1 n − 1 n − 2 n-2 n − 2 Θ ( n ) \Theta(n) Θ ( n ) O ( n ) O(n) O ( n ) O ( n 2 ) O(n^2) O ( n 2 )
还能不能更优?
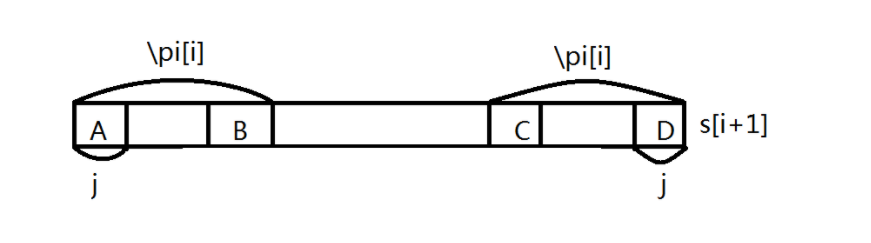
考虑当 s [ i + 1 ] s[i+1] s [ i + 1 ] s [ π [ i ] ] s[\pi[i]] s [ π [ i ] ] π [ i ] \pi[i] π [ i ] j j j i i i s [ i + 1 ] s[i+1] s [ i + 1 ] s [ j ] s[j] s [ j ] π [ i + 1 ] = j + 1 \pi[i+1]=j+1 π [ i + 1 ] = j + 1 j ( 2 ) j^{(2)} j ( 2 ) j = 0 j=0 j = 0 π [ i + 1 ] = 0 \pi[i+1]=0 π [ i + 1 ] = 0
画个图先:
首先我们知道 A 和 D 相同,然后由于 p i pi p i j = π [ π [ i ] − 1 ] j=\pi[\pi[i]-1] j = π [ π [ i ] − 1 ] j ( n ) = π [ j ( n − 1 ) − 1 ] j^{(n)}=\pi[j^{(n-1)}-1] j ( n ) = π [ j ( n − 1 ) − 1 ] O ( n ) O(n) O ( n ) π \pi π
时间复杂度咋证?
原来 O ( n 2 ) O(n^2) O ( n 2 ) Θ ( n ) \Theta(n) Θ ( n )
code:
1 2 3 4 5 6 7 8 9 10 11 12 13 vector<int > pf (string s) int n = (int )s.length ();vector<int > pi (n) ;for (int i = 1 ; i < n; i++)int j = pi[i - 1 ];while (j && s[i] != s[j]) j = pi[j - 1 ];if (s[i] == s[j]) j++;return pi;
这一块 OI-Wiki 上和 π \pi π
对于长度为 n n n s s s z [ i ] z[i] z [ i ] s s s s [ i … n − 1 ] s[i\dots n-1] s [ i … n − 1 ]
考虑如何求。暴力 O ( n 2 ) O(n^2) O ( n 2 ) i i i [ i … i + z [ i ] − 1 ] [i\dots i+z[i]-1] [ i … i + z [ i ] − 1 ] i i i i + z [ i ] − 1 i+z[i]-1 i + z [ i ] − 1 [ l … r ] [l\dots r] [ l … r ]
如果 i ≤ r i\leq r i ≤ r [ l , r ] [l,r] [ l , r ] z [ i ] ≥ min ( z [ i − l ] , r − i + 1 ) z[i]\geq \min(z[i-l],r-i+1) z [ i ] ≥ min ( z [ i − l ] , r − i + 1 )
如果 i ≥ r i\geq r i ≥ r z [ i ] z[i] z [ i ] [ l , r ] [l,r] [ l , r ]
这样做复杂度显然是 O ( n ) O(n) O ( n ) r r r
code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 vector<int > z_function (string s) int n = (int )s.length ();vector<int > z (n) ;for (int i = 1 , l = 0 , r = 0 ; i < n; i++)if (i <= r && z[i - l] < r - i + 1 ) z[i] = z[i - l];else max (0 , r - i + 1 );while (i + z[i] < n && s[i + z[i]] == s[z[i]]) ++z[i];if (i + z[i] - 1 > r) r = i + z[i] - 1 , l = i;return z;
把被匹配的串和匹配的串拼一块,算一遍 π \pi π
对于字符串 s s s 0 ≤ r < ∣ s ∣ 0\leq r<|s| 0 ≤ r < ∣ s ∣ r r r r r r s s s border \text{border} border
由 r r r s s s border \text{border} border ∣ s ∣ − r |s|-r ∣ s ∣ − r s s s n − π [ n − 1 ] n-\pi[n-1] n − π [ n − 1 ] s s s
先考虑前缀在其本身的字符串中出现的次数。首先对于 i i i π [ i ] \pi[i] π [ i ] i i i j ( n ) j^{(n)} j ( n )
1 2 3 4 vector<int > ans (n + 1 ) ;for (int i = 0 ; i < n; i++) ans[pi[i]]++;for (int i = n - 1 ; i >= 0 ; i--) ans[pi[i - 1 ]] += ans[i];for (int i = 0 ; i < n; i++) ans[i]++;
然后考虑前缀在另一个字符串中出现的次数,类比 kmp \text{kmp} kmp
迭代地考虑问题,考虑把字符一个个往串里加怎么更新答案。令当前的答案为 k k k c c c s s s t = s c t=sc t = s c t ∼ t\sim t ∼ t t t c c c t ∼ t\sim t ∼ ∣ s ∣ + 1 − π max |s|+1-\pi_{\max} ∣ s ∣ + 1 − π m a x O ( n 2 ) O(n^2) O ( n 2 ) O ( n 2 ) O(n^2) O ( n 2 )
当然,你还可以把前缀函数建出一个自动机,但这个后面再说(或者永远不说)。
OI 中所说的“自动机”一般都指“确定有限状态自动机”,也就是 dfa \text{dfa} dfa kmp \text{kmp} kmp
写这一部分的时候主要参考了 qyc 在 SDSC2024 的讲义以及 qyc 的博客 。
感性理解,dfa \text{dfa} dfa
形式化地,一个 dfa \text{dfa} dfa
字符集 Σ \Sigma Σ
状态集合 Q Q Q dfa \text{dfa} dfa
起始状态 s t a r t , s t a r t ∈ Q start,start\in Q s t a r t , s t a r t ∈ Q
接受状态集合 F F F
转移函数 δ \delta δ
如果 dfa \text{dfa} dfa A A A S S S A ( S ) = True A(S)=\text{True} A ( S ) = True A ( S ) = False A(S)=\text{False} A ( S ) = False
如果一个 dfa \text{dfa} dfa dfa \text{dfa} dfa 接受 ,否则说这个 dfa \text{dfa} dfa 不接受 这个字符串。
如果一个状态 v v v c c c δ ( v , c ) = null \delta(v,c)=\text{null} δ ( v , c ) = null null \text{null} null null \text{null} null
我们扩展定义 δ \delta δ δ ( v , s ) = δ ( δ ( v , s [ 0 ] ) , s [ 1 … n − 1 ] ) \delta(v,s)=\delta(\delta(v,s[0]),s[1\dots n-1]) δ ( v , s ) = δ ( δ ( v , s [ 0 ] ) , s [ 1 … n − 1 ] ) A ( s ) = [ δ ( s t a r t , s ) ∈ F ] A(s)=[\delta(start,s)\in F] A ( s ) = [ δ ( s t a r t , s ) ∈ F ]
dfa \text{dfa} dfa dp \text{dp} dp dfa \text{dfa} dfa
如果有两个 dfa \text{dfa} dfa dfa \text{dfa} dfa dfa \text{dfa} dfa dfa \text{dfa} dfa
nfa \text{nfa} nfa dfa \text{dfa} dfa nfa \text{nfa} nfa 2 n 2^n 2 n dfa \text{dfa} dfa
这里的最小化指的是规模上的最小化。
如果两个状态的所有转移都是对应相同的,称这两个状态等价。我们尝试把这两个状态合并起来。
朴素的做法就是把每个状态的转移 Hash \text{Hash} Hash O ( n 2 Σ ) O(n^2\Sigma) O ( n 2 Σ )
考虑一个更快的方法。既然合并慢,那就分裂。我们在一开始把接受状态合并起来,把拒绝状态合并起来,考虑如果两个状态的同一转移指向了不同的等价类,那么就把这两个状态分裂开。这个算法叫做 moore \text{moore} moore O ( n ( Σ + log n ) ) O(n(\Sigma+\log n)) O ( n ( Σ + log n ) ) dfa \text{dfa} dfa O ( n 2 Σ ) O(n^2\Sigma) O ( n 2 Σ )
类似于 SPFA 优化 Bellman-Ford,我们维护一个队列,把每一次分裂后新增的等价类放进去。关键的优化是,我们把一个等价类 x x x y , z y,z y , z y , z y,z y , z x x x x x x y , z y,z y , z O ( n Σ log n ) O(n\Sigma\log n) O ( n Σ log n )
就是在 trie 上 kmp。每个节点维护 fail 指针指向 trie 上最深的点满足它是当前点所代表的串的前缀。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 namespace acamconst int SIZ = 2000005 ;struct node int ch[26 ], fail, ans, id;node () { memset (ch, 0 , sizeof (ch)), ans = id = 0 ; }inline int &operator [](const int x) { return x < 26 ? ch[x] : ch[x - 'a' ]; }inline int operator [](const int x) const { return x < 26 ? ch[x] : ch[x - 'a' ]; }int tot, ans[SIZ], pcnt;int > fail[SIZ];inline void insert (char *s, int &id) int u = 0 ;for (int i = 1 ; s[i]; i++)if (!tr[u][i]) tr[u][i] = ++tot;if (!tr[u].id) tr[u].id = ++pcnt;inline void build () int > q;for (int i = 0 ; i < 26 ; i++)if (tr[0 ][i]) q.push (tr[0 ][i]), fail[0 ].push_back (tr[0 ][i]);while (!q.empty ())int u = q.front ();pop ();for (int i = 0 ; i < 26 ; i++)if (tr[u][i])push_back (tr[u][i]);push (tr[u][i]);else tr[u][i] = tr[tr[u].fail][i];void query (char *t) int u = 0 ;for (int i = 1 ; t[i]; ++i) u = tr[u][t[i]], tr[u].ans++;void dfs (int u) for (int v : fail[u])dfs (v);
子序列自动机是接受且仅接受一个字符串的子序列的自动机。构造方式:
状态 i i i s [ 1 … i ] s[1\dots i] s [ 1 … i ] s [ 1 … i − 1 ] s[1\dots i-1] s [ 1 … i − 1 ]
自动机上每个状态都是接受状态。
转移 δ ( u , c ) = min { i ∣ i > u , s [ i ] = c } \delta(u,c)=\min\{i|i>u,s[i]=c\} δ ( u , c ) = min { i ∣ i > u , s [ i ] = c }
构造的时候从后往前扫描,时间复杂度 O ( n ∣ Σ ∣ ) O(n|\Sigma|) O ( n ∣ Σ ∣ )
后缀数组 s a [ i ] sa[i] s a [ i ] i i i r k [ i ] rk[i] r k [ i ] i i i r k [ i ] rk[i] r k [ i ] s a [ r k [ i ] ] = r k [ s a [ i ] ] = i sa[rk[i]]=rk[sa[i]]=i s a [ r k [ i ] ] = r k [ s a [ i ] ] = i
比较通用的做法是利用倍增,时间复杂度 O ( n log n ) O(n\log n) O ( n log n )
参考了 应该是发现者的论文 。
DC3 Algorithm 是用来求后缀数组的 O ( n ) O(n) O ( n ) O ( n log n ) O(n\log n) O ( n log n )
自然的想法是把串二分,但是最好也只是 O ( n log n ) O(n\log n) O ( n log n ) i m o d 3 = 0 i\bmod 3=0 i m o d 3 = 0
第一步,求解 B 类后缀,对于每个后缀用前三个字符进行比较,也就是做三轮基数排序,如果比出来了就结束,否则用以 i i i i m o d 3 = 1 i\bmod 3=1 i m o d 3 = 1 i m o d 3 = 2 i\bmod 3=2 i m o d 3 = 2
第二步,求解 A 类后缀,发现 A 类后缀是由一个 A 类字符和一个 B 类后缀构成的,于是以当前字符为第一关键字,B 类后缀为第二关键字再做基数排序就行了。
第三步,将 A 与 B 归并起来。假设归并到 A 的下标为 i i i j j j s [ i ] ≠ s [ j ] s[i]\not=s[j] s [ i ] = s [ j ] j m o d 3 = 1 j\bmod 3=1 j m o d 3 = 1 j + 1 j+1 j + 1 i + 1 i+1 i + 1 j m o d 3 = 2 j\bmod 3=2 j m o d 3 = 2 j + 1 j+1 j + 1 i + 1 i+1 i + 1
这样通过巧妙的三步,我们就可以求出 s a sa s a
如何证明时间复杂度?
有递归式 T ( n ) = Θ ( n ) + T ( 2 3 n ) T(n)=\Theta(n)+T(\frac{2}{3}n) T ( n ) = Θ ( n ) + T ( 3 2 n ) T ( n ) = Θ ( n ) T(n)=\Theta(n) T ( n ) = Θ ( n )
参考了 A Walk Through the SA-IS Algorithm 。
这也是一种 O ( n ) O(n) O ( n )
记 S ( i ) S(i) S ( i ) i i i S ( i ) < S ( i + 1 ) S(i)<S(i+1) S ( i ) < S ( i + 1 ) S ( i ) > S ( i + 1 ) S(i)>S(i+1) S ( i ) > S ( i + 1 )
定义一种特殊的 S-type 后缀 lm-type 后缀表示一连串的 S-type 后缀中最左边的那个。定义 LMS 子串表示位置相邻的两个 lm-type 后缀的起始位置之间的所有字符(不包括第二个 lm-type 后缀的起始字符)。容易知道所有 LMS 子串的数量不超过 ∣ S ∣ / 2 |S|/2 ∣ S ∣ / 2 O ( ∣ S ∣ ) O(|S|) O ( ∣ S ∣ ) O ( ∣ S ∣ ) O(|S|) O ( ∣ S ∣ )
我们可以先把 lm-type 的东西排出来,然后用顺序重命名它,放在新串 s 1 s1 s 1 s a ′ sa' s a ′
我们需要意识到的是让问题变难的正是这些 lm-type 后缀,所以我们先假设这些后缀已经被排好了,得到的后缀数组为 s a ′ sa' s a ′ 诱导排序 的方法排序。注意到同种字符开头的排序后肯定放在了一块,并且其内部是 L-type 在前,S-type 在后,于是利用桶排序的思想,记录每种字符的出现次数,并且在 sa 中分配相应的空间,相当于是拿 sa 开了个桶。先倒序扫描 s a ′ sa' s a ′ s a [ i ] − 1 sa[i]-1 s a [ i ] − 1 s a [ i ] − 1 sa[i]-1 s a [ i ] − 1 s a [ i ] − 1 sa[i]-1 s a [ i ] − 1 s a [ i ] − 1 sa[i]-1 s a [ i ] − 1
然后需要考虑 LMS 子串的排序。鸡排是可以的,但是常数太大,为了展现 SA-IS 的优越性,仍然使用诱导排序。然后就做完了。
有递归式 T ( n ) = Θ ( n ) + T ( n 2 ) T(n)=\Theta(n)+T(\frac{n}{2}) T ( n ) = Θ ( n ) + T ( 2 n ) T ( n ) = Θ ( n ) T(n)=\Theta(n) T ( n ) = Θ ( n )
在 LOJ #111 后缀排序 的提交记录中,O ( n log n ) O(n\log n) O ( n log n )
定义两个字符串 S S S T T T S S S lcp ( i , j ) \operatorname{lcp}(i,j) l c p ( i , j ) i i i j j j
定义 height 数组 h e i g h t [ i ] = lcp ( s a [ i ] , s a [ i − 1 ] ) height[i]=\operatorname{lcp}(sa[i],sa[i-1]) h e i g h t [ i ] = l c p ( s a [ i ] , s a [ i − 1 ] ) h e i g h t [ 0 ] height[0] h e i g h t [ 0 ]
引理 :h e i g h t [ r k [ i ] ] ≥ h e i g h t [ r k [ i − 1 ] ] − 1 height[rk[i]]\geq height[rk[i-1]]-1 h e i g h t [ r k [ i ] ] ≥ h e i g h t [ r k [ i − 1 ] ] − 1
proof. \text{proof.} proof.
当 h e i g h t [ r k [ i − 1 ] ] ≤ 1 height[rk[i-1]]\leq 1 h e i g h t [ r k [ i − 1 ] ] ≤ 1 RHS ≤ 0 \text{RHS}\le 0 RHS ≤ 0
当 h e i g h t [ r k [ i − 1 ] ] > 1 height[rk[i-1]]>1 h e i g h t [ r k [ i − 1 ] ] > 1 lcp ( s a [ r k [ i − 1 ] ] , s a [ r k [ i − 1 ] − 1 ] ) > 1 \operatorname{lcp}(sa[rk[i-1]],sa[rk[i-1]-1])>1 l c p ( s a [ r k [ i − 1 ] ] , s a [ r k [ i − 1 ] − 1 ] ) > 1 i − 1 i-1 i − 1 s a [ r k [ i − 1 ] − 1 ] sa[rk[i-1]-1] s a [ r k [ i − 1 ] − 1 ] h e i g h t [ r k [ i − 1 ] ] height[rk[i-1]] h e i g h t [ r k [ i − 1 ] ] a A aA a A i − 1 i-1 i − 1 a A B aAB a A B s a [ r k [ i − 1 ] − 1 ] sa[rk[i-1]-1] s a [ r k [ i − 1 ] − 1 ] a A D aAD a A D i i i A B AB A B S A [ r k [ i − 1 ] − 1 ] + 1 SA[rk[i-1]-1]+1 S A [ r k [ i − 1 ] − 1 ] + 1 A D AD A D
可知 A D ≤ 后缀 s a [ r k [ i ] − 1 ] ≤ A B AD\leq 后缀 sa[rk[i]-1]\leq AB A D ≤ 后 缀 s a [ r k [ i ] − 1 ] ≤ A B i i i s a [ r k [ i ] − 1 ] sa[rk[i]-1] s a [ r k [ i ] − 1 ] □ \square □
于是利用上面的引理,可以 O ( n ) O(n) O ( n )
1 2 3 4 5 6 7 for (int i = 0 , k = 0 ; i < n; i++)if (!rk[i]) continue ;if (k) --k;while (s[i + k] == s[sa[rk[i] - 1 ] + k]) ++k;
有 LCP Lemma:
∀ s a [ i ] < s a [ j ] < s a [ k ] , lcp ( s a [ i ] , s a [ k ] ) = min ( lcp ( s a [ i ] , s a [ j ] ) , lcp ( s a [ j ] , s a [ k ] ) ) \forall sa[i]<sa[j]<sa[k],\operatorname{lcp}(sa[i],sa[k])=\min(\operatorname{lcp}(sa[i],sa[j]),\operatorname{lcp}(sa[j],sa[k]))
∀ s a [ i ] < s a [ j ] < s a [ k ] , l c p ( s a [ i ] , s a [ k ] ) = min ( l c p ( s a [ i ] , s a [ j ] ) , l c p ( s a [ j ] , s a [ k ] ) )
可利用其推出 LCP Theorem:
lcp ( s a [ i ] , s a [ j ] ) = min { h e i g h t [ i + 1 … j ] } \operatorname{lcp}(sa[i],sa[j])=\min\{height[i+1\dots j]\}
l c p ( s a [ i ] , s a [ j ] ) = min { h e i g h t [ i + 1 … j ] }
感性理解一下就是 height 数组一直大于的一个数就是反复出现的前缀。
利用 LCP Theorem,可以将子串公共前缀问题转化为 RMQ 问题。